Problemy nieefektywności w transporcie miejskim
Użytkownik będzie zatem dokonywał wyboru jednej spośród danego zbioru alternatyw. Każdej z nich przypisze on pewną użyteczność (uzależnioną od swoich preferencji) i wybierze optymalną, tzn. tę o najwyższej użyteczności. O ile jednak podróżujący zna własną użyteczność dla poszczególnych alternatyw, o tyle badacz nie ma co do niej pewności. Wynika to z faktu, że mogą na nią mieć wpływ czynniki nieobserwowalne (bądź nieuwzględnione przez model) oraz z błędów pomiaru czynników obserwowalnych. Dlatego też użyteczność przypisywaną alternatywie i przez daną osobę modelowana jest jako zmienna losowa:

W powyższym równaniu Vi to deterministyczna część użyteczności (określana też jako użyteczność mierzalna bądź systematyczna), a E_i jest składnikiem losowym odpowiadającym wspomnianym nieobserwowalnym czynnikom i błędom pomiaru. Tak sformułowany model jest liniową wersją losowego modelu użyteczności (Random Utility Model – RUM11).
Najprostszą możliwością jest wybór spośród dwóch alternatyw, oznaczymy je przez 0 i 1. Prawdopodobieństwo wybrania alternatywy 1 wynosi:
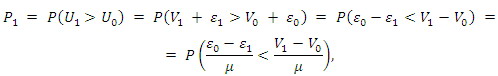
gdzie µ jest parametrem dobranym tak, by (E_0-E_1)/µ miało rozkład normalny. Wówczas dla F będącej dystrybuantą rozkładu normalnego mamy P_1 = F((V_1-V_0)/µ). Oznacza to, że prawdopodobieństwo wybrania alternatywy 1 jest rosnącą funkcją różnicy między jej mierzalną użytecznością a mierzalną użytecznośc
ią „konkurencyjnej” alternatywy 0.
Forma funkcyjna zależy od założonego a priori rozkładu E_0 i E_1. Najczęściej wybierane są rozkład Gumbela (podwójny wykładniczy) i normalny – mają one podobny kształt – które prowadzą odpowiednio do modeli logit i probit. Omawiane dalej przykłady oparte będą na modelu logitowym mającym tę przewagę, że prawdopodobieństwa można wyznaczyć analitycznie.
Dystrybuanta rozkładu Gumbela ma postać F(E) = exp(-e^(-E)). Jeśli E_0 i E_1 są niezależnymi zmiennymi losowymi o tym samym rozkładzie Gumbela, to ich różnica E_0 – E_1 ma rozkład logistyczny. Wtedy prawdopodobieństwo wyboru alternatywy 1 wynosi:

przy czym ∆V = V_o-V_1, a P_1 jest rosnącą funkcją ∆V i wynosi 0,5 dla ∆V = 0 (co oznacza, że przy równych mierzalnych użytecznościach obu alternatyw prawdopodobieństwo wyboru pierwszej wynosi 0,5). Zwróćmy uwagę na to, że dla niskich wartości µ model jest niemal deterministyczny i w zależności od znaku stojącego przy wielkości ∆V (o ile różni się ona znacząco od 0) P1 będzie bliskie 0 lub 1. Przy wysokich wartościach µ będziemy mieli natomiast P1 = 0,5 nawet dla wysokich absolutnych wartości ∆V. Oznacza to, że walory prognostyczne modelu mogą być w pewnych sytuacjach ograniczone.

W powyższym równaniu Vi to deterministyczna część użyteczności (określana też jako użyteczność mierzalna bądź systematyczna), a E_i jest składnikiem losowym odpowiadającym wspomnianym nieobserwowalnym czynnikom i błędom pomiaru. Tak sformułowany model jest liniową wersją losowego modelu użyteczności (Random Utility Model – RUM11).
Najprostszą możliwością jest wybór spośród dwóch alternatyw, oznaczymy je przez 0 i 1. Prawdopodobieństwo wybrania alternatywy 1 wynosi:
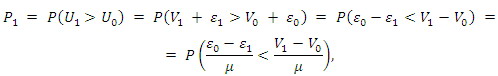
gdzie µ jest parametrem dobranym tak, by (E_0-E_1)/µ miało rozkład normalny. Wówczas dla F będącej dystrybuantą rozkładu normalnego mamy P_1 = F((V_1-V_0)/µ). Oznacza to, że prawdopodobieństwo wybrania alternatywy 1 jest rosnącą funkcją różnicy między jej mierzalną użytecznością a mierzalną użytecznośc
Dystrybuanta rozkładu Gumbela ma postać F(E) = exp(-e^(-E)). Jeśli E_0 i E_1 są niezależnymi zmiennymi losowymi o tym samym rozkładzie Gumbela, to ich różnica E_0 – E_1 ma rozkład logistyczny. Wtedy prawdopodobieństwo wyboru alternatywy 1 wynosi:

przy czym ∆V = V_o-V_1, a P_1 jest rosnącą funkcją ∆V i wynosi 0,5 dla ∆V = 0 (co oznacza, że przy równych mierzalnych użytecznościach obu alternatyw prawdopodobieństwo wyboru pierwszej wynosi 0,5). Zwróćmy uwagę na to, że dla niskich wartości µ model jest niemal deterministyczny i w zależności od znaku stojącego przy wielkości ∆V (o ile różni się ona znacząco od 0) P1 będzie bliskie 0 lub 1. Przy wysokich wartościach µ będziemy mieli natomiast P1 = 0,5 nawet dla wysokich absolutnych wartości ∆V. Oznacza to, że walory prognostyczne modelu mogą być w pewnych sytuacjach ograniczone.
11. T. Magnac, Logit models of individual choices, 2005, s. 1, publikacja dostępna na stronie: http://idei.fr/doc/by/magnac/logit.pdf

