Problemy nieefektywności w transporcie miejskim
1.7. Rozwiązanie przykładu liczbowego
Wróćmy do rozważanego wcześniej przykładu. Założymy stałą sumę popytów (równą 300 000) i liniowość funkcji d1(p1), d2(p1), P2(q2). Jako że poznaliśmy już wartości tych funkcji dla dwóch przypadków p1 = 4 USD i p2 = 2 USD, możemy je wyznaczyć.

Zatem:
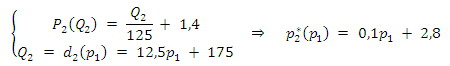
Krańcowe koszty społeczne transportu masowego MSC_1 wynoszą 4. Krańcowy koszt transportu samochodowego wyznaczymy z posiadanych danych:
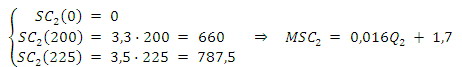
Przy tym wyprowadzenie MSC_2 uzyskaliśmy ze wzoru:
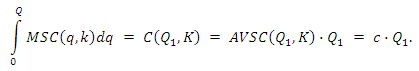
Korzystając z Q_2 = d_2 (p_1 ) = 12,5p_1 + 175, możemy następnie otrzymać MSC_2 jako funkcję zmiennej p1:
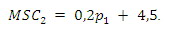
Teraz już, podstawiając uzys
kane zależności do równania:
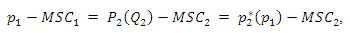
mamy:
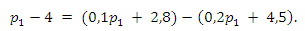
Stąd:
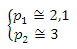
Warto tu zwrócić uwagę na fakt, że ceny te nie są optymalne (w sensie ogólnym), gdyż różnią się od kosztów społecznych. Jest to spowodowane zaburzeniem wprowadzonym przez regułę cenową p_2 = Q_2/125 + 1,4 = 0,1p_1 + 2,8, które uniemożliwia osiągnięcie optimum. Okazuje się w związku z tym, że subsydium prowadzące do obniżenia ceny transportu o niemal połowę (czyli w przybliżeniu tak jak w rozważanym powyżej przykładzie) w stosunku do kosztów jest drugim najlepszym rozwiązaniem (second-best optimal).
Kolejnym spostrzeżeniem, jakie możemy tu poczynić, jest to, że przy założeniu wyższych kosztów zewnętrznych w transporcie samochodowym i niższego kosztu transportu masowego (tzn. w równaniu p_1 - MSC_1 = P_2 (Q_2 )- MSC_2 mielibyśmy wyższe MSC_2 i niższe MSC_1) cena transportu masowego w zaburzonej równowadze mogłaby nawet być ujemna.
Wróćmy do rozważanego wcześniej przykładu. Założymy stałą sumę popytów (równą 300 000) i liniowość funkcji d1(p1), d2(p1), P2(q2). Jako że poznaliśmy już wartości tych funkcji dla dwóch przypadków p1 = 4 USD i p2 = 2 USD, możemy je wyznaczyć.

Zatem:
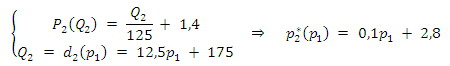
Krańcowe koszty społeczne transportu masowego MSC_1 wynoszą 4. Krańcowy koszt transportu samochodowego wyznaczymy z posiadanych danych:
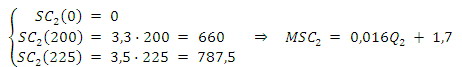
Przy tym wyprowadzenie MSC_2 uzyskaliśmy ze wzoru:
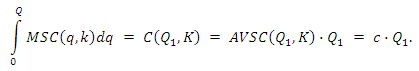
Korzystając z Q_2 = d_2 (p_1 ) = 12,5p_1 + 175, możemy następnie otrzymać MSC_2 jako funkcję zmiennej p1:
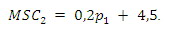
Teraz już, podstawiając uzys
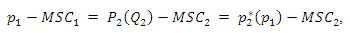
mamy:
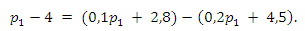
Stąd:
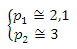
Warto tu zwrócić uwagę na fakt, że ceny te nie są optymalne (w sensie ogólnym), gdyż różnią się od kosztów społecznych. Jest to spowodowane zaburzeniem wprowadzonym przez regułę cenową p_2 = Q_2/125 + 1,4 = 0,1p_1 + 2,8, które uniemożliwia osiągnięcie optimum. Okazuje się w związku z tym, że subsydium prowadzące do obniżenia ceny transportu o niemal połowę (czyli w przybliżeniu tak jak w rozważanym powyżej przykładzie) w stosunku do kosztów jest drugim najlepszym rozwiązaniem (second-best optimal).
Kolejnym spostrzeżeniem, jakie możemy tu poczynić, jest to, że przy założeniu wyższych kosztów zewnętrznych w transporcie samochodowym i niższego kosztu transportu masowego (tzn. w równaniu p_1 - MSC_1 = P_2 (Q_2 )- MSC_2 mielibyśmy wyższe MSC_2 i niższe MSC_1) cena transportu masowego w zaburzonej równowadze mogłaby nawet być ujemna.

